Teori graf merupakan salah satu cabang ilmu matematika dalam bidang Aljabar. Graf terdiri dari himpunan titik dan himpunan sisi dengan syarat himpunan titik tidak boleh kosong. Sedangkan himpunan sisi memuat pasangan tak teurut dua titil yang berbeda. Teori graf pertama kali diperkenalkan oleh Leonhard Euler pada tahun 1736 melalui tulisan Euler yang berisi tentang upaya pemecahan masalah jembatan Königsberg di Eropa.
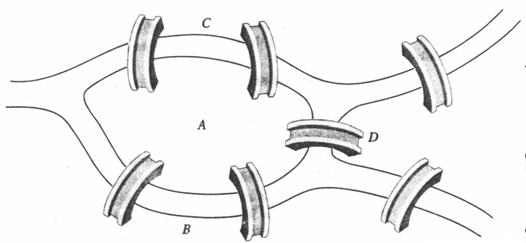
Di kota Königsberg (sekarang Kaliningrad) terdapat sungai Pregel yang melalui kota Königsberg membagi wilayah daratan pada kota tersebut menjadi empat bagian. Tujuh buah jembatan dibangun di atas sungai Pregel pada bagian yang memungkinkan untuk bepergian antar keempat wilayah tersebut. Pada abad ke-17, dirancang rute perjalanan yang melintasi kota di empat daratan, yang melintasi masing-masing dari tujuh jembatan tepat satu kali.
Pada tahun 1736, seorang pakar matematika ternama, Leonhard Euler menulis sebuah artikel yang membahas tidak hanya solusi atas teka-teki Königsberg semata, akan tetapi juga dilengkapi dengan metode umum untuk persoalan serupa lainnya. Untuk memecahkan masalah itu, Euler memisalkan daratan yang dinyatakan dengan titik (vertex) dan jembatan dinyatakan dengan garis atau sisi (edge).
Euler berkesimpulan bahwa tidak mungkin seseorang dapat melalui ketujuh jembatan itu masing-masing tepat satu kali dalam perjalannya menuju keempat daratan tersebut. Konsep yang digunakan dalam menyelesaikan pembuktian dari kejadian inilah yang dijadikan sebagai permulaan dari teori graf.
Pada waktu setelahnya teori ini telah berkembang secara teoritis. Seperti diketahui, bahwa perkembangan teoritis untuk mengembangkan suatu model matematika harus berada di depan dibandingkan permasalahan-permasalahan empiris. Hal ini karena kajian matematika teori tidak hanya dapat diaplikasikan bagi satu permasalahan saja, melainkan pada berbagai bidang yang memiliki bentuk yang sama.
Salah satu perkembangannya adalah tentang konsep dimensi metrik dibangun oleh Harary pada tahun 1976, konsep ini berkembang pesat melalui dua jalur, yaitu jalur terapan dan jalur teori. Melalui jalur terapan di antaranya adalah pada navigasi robot yang medan geraknya disajikan dalam bentuk graf dan penempatan alarm kebakaran yang posisi penempatannya disajikan dalam bentuk graf. Perkembangan melalui jalur teori diarahkan pada pengembangan berbagai jenis dimensi graf dan penerapannya pada berbagai graf.
Saat ini telah muncul beberapa jenis diantaranya dimensi metrik lokal, dimensi metrik ketetanggaan, dimensi metrik lokal ketetanggaan, dan dimensi metrik komplemen. Perkembangan selanjutnya dilakukan oleh Arumugam dan Mathew (2012) yang memperkenalkan dimensi metrik lainnya, yaitu dimensi metrik fraksional.
Berbagai jenis dimensi metrik ini kemudian diterapkan pada berbagai graf, baik graf tunggal, seperti graf lengkap, graf pohon, dan graf bipartit maupun graf hasil operasi, seperti operasi hasil kali korona, kom, dan kartesius. Sebagaimana dimensi metrik yang telah dperkenalkan sebelumnya, dimensi metrik fraksional juga dikembangkan di antaranya ke dimensi metrik fraksional dan dimensi metrik fraksional lokal. Perbedaan keduanya terletak pada pasangan titik yang digunakan. Jika dimensi metrik fraksional melibatkan fungsi pembeda dari semua pasangan sebarang dua titik, maka dimensi metrik fraksional lokal melibatkan fungsi pembeda dari semua pasangan titik yang bertetangga.
Dimensi metrik fraksional lokal merupakan jumlah minimal bobot semua titik pada graf dengan bobot bilangan riil antara 0 sampai 1. Jumlah minimal tersebut harus memenuhi kendala semua fungsi pembeda lokal dari setiap dua titik yang bertetangga dan mempunyai nilai lebih dari atau sama dengan satu.
Pada penelitian ini diperoleh empat teorema baru. Teorema pertama dimensi metrik fraksional lokal dari graf lintasan, graf lengkap, graf sikel, graf bintang, dan graf bipartite berordo n berturut-turut adalah 1; n/2; n/(n-1) jika n gasal dan 1 jika n genap; 1; 1.Teorema kedua dimensi metrik fraksional lokal dari hasil kali korona graf terhubung non trivial G dan graf kosong H sama dengan dimensi metrik fraksional dari G.
Teorema ketiga dimensi metrik fraksional lokal dari graf terhubung G dan graf H sama dengan kardinalitas himpunan titik graf G kali dimensi metrik fraksional lokal dari H. Teorema keempat memiliki dua bagian, (1) dimensi metrik fraksional lokal dari hasil kali G korona H sama dengan kardinalitas dari himpunan titik G dikalikan dimensi fraksional lokal dari K1 ditambah H dengan K1 bukan anggota sebarang basis metrik lokal dari K1 ditambah H; (2) dimensi metrik fraksional lokal dari hasil kali G korona H sama dengan kardinalitas dari himpunan titik G dikalikan dengan dimensi fraksional lokal dari K1 ditambah H dikurangi 1, dengan K1 merupakan anggota sebarang basis metrik lokal dari K1 ditambah H.
Penulis: Mohammad Imam Utoyo
Artikel lebih lengkap dapat diakses melalui laman berikut,
https://iopscience.iop.org/article/10.1088/1755-1315/243/1/012043/meta