Model regresi linier biasa (RLB) selama ini telah menjadi sebuah metode yang ampuh untuk analisis regresi. Beberapa asumsi yang diberlakukan diantaranya adalah adanya independensi antar satuan pengamatan dan adanya keseragaman satuan pengamatan. Dalam model RLB ini, parameter regresi diatur seragam atau konstan atas semua satuan pengamatan.
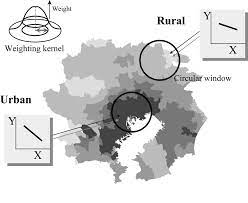
Untuk data spasial, yaitu data yang memuat informasi lokasi geografis sebagai satuan pengamatan, umumnya terdapat dependensi antar lokasi pengamatan dan keberagaman karakteristik di tiap-tiap lokasi pengamatan. Fakta tersebut tidak sesuai dengan asumsi model RLB. Dengan demikian, penerapan model RLB pada data spasial tidak realistis. Oleh karena itu, pada data spasial RLB dikembangkan dengan cara membuat parameter regresi bervariasi antar lokasi atau satuan pengamatan. Pemodelan yang demikian disebut Geographically Weighted Regression (GWR). Dengan cara demikian, model GWR mengakomodasi keberagaman antar satuan pengamatan. Disamping itu, estimasi parameter model juga dilakukan di tiap satuan pengamatan dengan mempertimbangkan dependensi satuan pengamatan yang lain. Dependensi tersebut diakomodasi dengan cara memberikan bobot yang berbeda kepada satuan pengamatan yang lain berdasarkan jarak lokasinya.
Model GWR merupakan daya tarik yang besar dalam analisis data spasial di berbagai bidang seperti klimatologi, ekonometrik, epidemiologi, dan ilmu lingkungan. Namun, perlu diperhatikan bahwa model GWR merupakan pengembangan dari model RLB. Artinya, variabel responsnya di setiap lokasi dimodelkan sebagai fungsi linier dari sekumpulan variabel penjelas. Dalam kehidupan nyata, ada banyak bukti bahwa hubungan antara variabel respon dan prediktor bersifat nonlinier. Oleh karena itu, diperlukan pengembangan model GWR yang dapat mengakomodasi respon dalam variabel kontinu dan memiliki hubungan nonlinier dengan satu atau lebih variabel penjelas.
Untuk mengatasi masalah di atas, telah diusulkan suatu pengembangan model GWR dengan menggunakan pendekatan fungsi polinomial. Model pengembangan tersebut dinamakan Geographically Weighted Polynomial Regression (GWPolR). Pada studi perbandingan berdasarkan data empiris, indikator kesesuaian model yang dihasilkan oleh model GWPolR secara angka lebih baik dibandingkan dengan model GWR. Namun demikian, belum dapat dinyatakan secara statistik bahwa GWPolR secara signifikan lebih baik daripada GWR dalam kasus-kasus tersebut. Jadi, untuk mengkonfirmasi secara statistika harus digunakan uji statistik. Oleh karena itu, tujuan dari penelitian ini adalah untuk membangun prosedur uji kesesuaian model GWPolR dan mengevaluasi kinerja atau performanya.
Dalam penelitian ini, uji kesesuaian model dibangun untuk memutuskan apakah GWPolR secara signifikan lebih baik daripada model GWR dalam mendeskripsikan data sampel yang diberikan. Hipotesis untuk uji tersebut adalah H0: Model GWPolR tidak lebih baik daripada model GWR untuk data sampel yang diberikan melawan H1: Model GWPolR secara signifikan lebih baik daripada model GWR untuk data sampel yang diberikan. Untuk menguji hipotesis tersebut, statistik uji dibangun berdasarkan jumlah kuadrat residual dari kedua model yang dibandingkan. Terdapat beberapa cara merumuskan statistik uji. Dalam penelitian ini, statistik uji dirumuskan sebagai rasio antara jumlah kuadrat residual model GWPolR dengan model GWR. Distribusi probabilitas dari jumlah kuadrat residual masing-masing model dapat didekati dengan distribusi Chi-Square. Oleh karena itu, distribusi dari statistik uji yang merupakan rasio dari Chi-Square dapat didekati dengan pendekatan distribusi F. Selanjutnya, distribusi F ini dapat digunakan untuk menentukan keputusan uji.
Untuk menilai performa uji maka dalam penelitian ini dilakukan simulasi. Dalam simulasi ini data dibangkitkan dari dua model. Pertama, data mengikuti model GWR. Sedangkan yang kedua, data mengikuti model GWPolR. Berdasarkan simulasi dengan 500 ulangan, ketika data dibangkitkan dari model GWR (di sini H0 adalah benar) maka tingkat penolakan hipotesis nol adalah 0%, atau dengan kata lain tingkat penerimaan adalah 100% dengan rata-rata p-value sebesar 0,8074. Di sisi lain, ketika data dibangkitkan dari model GWPolR (di sini H0 adalah salah) maka terjadi tingkat penolakan mulai dari 34% hingga 100% seiring bertambahnya ukuran sampel, dengan rata-rata p-value sebesar 0,0162. Dengan kata lain, dalam skema ini prosedur uji cenderung menolak hipotesis nol dan menyatakan bahwa GWPolR secara signifikan lebih baik daripada model GWR.
Ini artinya keputusan tes sudah sesuai dengan model yang sebenarnya. Berdasarkan simulasi, prosedur uji kesesuaian model telah bekerja dengan baik untuk memeriksa model terkait. Prosedur ini cukup efektif untuk mendeteksi model yang sesuai dengan data yang dibangkitkan atau diberikan.
Penulis: Dr. Toha Saifudin, M.Si.
Informasi detail dari riset ini dapat dilihat pada tulisan kami di:
https://aip.scitation.org/doi/abs/10.1063/5.0042125
Toha Saifudin, Fatmawati and Nur Chamidah (2021). The Performance of Goodness of Fit Test Procedure on Geographically Weighted Polynomial Regression Model. AIP Conference Proceedings, 2329, 060015: 060015-1 – 060015-10;