Teori graf merupakan salah satu cabang ilmu matematika dalam bidang Aljabar. Graf terdiri dari himpunan titik dan himpunan sisi dengan syarat himpunan titik tidak boleh kosong. Sedangkan himpunan sisi memuat pasangan tak teurut dua titik yang berbeda. salah satu penggunaan graf adalah pewarnaan graf. Pengertian dari pewarnaan graf adalah proses pemberian warna pada titik atau garis dengan persyaratan tertentu. Salah satu contoh dari pewarnaan graf adalah penjadwalan dalam bidang akademik. Misalkan sebuah Program Studi Pendidikan Matematika memiliki 10 (sepuluh) dosen.
Dosen pada Prodi Pendidikan Matematika tersebut direpresentasikan sebagai titik, yaitu a, b, c, d, e, f, g, h, i dan j. Dalam penerapan Pembelajaran Berbasis Riset (PBR), Kaprodi meminta setiap dosen harus memilih minimal 2 (dua) kelompok riset. Dosen dalam satu kelompok riset direpresentasikan sebagai sisi.
Setiap dosen dalam PBR tersebut harus mengintegrasikan masalah-masalah penelitiannya dalam perkuliahan. Agar proses pembelajaran dalam perkuliahan efektif, maka setiap dosen harus menerapkan dua atau lebih model pembelajaran dalam perkuliahan dengan syarat dosen dalam satu kelompok riset tidak boleh memilih model pembelajaran yang sama.
Dalam pemilihan dua atau lebih model pembelajaran untuk setiap dosen dengan mengoptimalkan model pembelajaran yang diterapkan dan dosen dalam satu kelompok riset tidak boleh memilih model pembelajaran yang sama. Model pembelajaran yang dipilih boleh sama bila kedua dosen tidak dalam satu kelompok riset. Bila setiap dosen harus memilih 2 (dua) atau 4 (empat) model pembelajaran dengan ketentuan yang sama, maka untuk menentukan model pembelajaran yang optimal yang diterapkan dosen, dapat dilakukan pemberian warna.
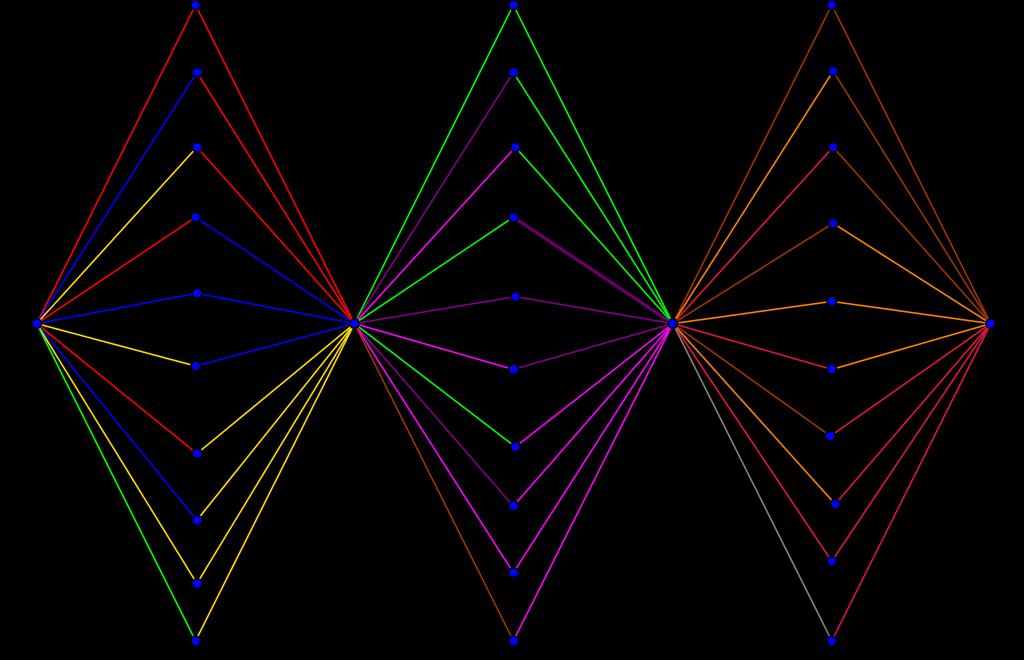
Proses pemberian warna titik ini dinamakan dengan pewarnaan titik pada graf. Pada saat kaprodi meminta setiap dosen memilih dua model pembelajaran, dosen a, b, dan i memiliki warna yang sama, yang berarti model pembelajaran yang dipilih bisa sama dan ketiga dosen tidak dalam satu kelompok riset. Apabila setiap dosen diminta untuk memilih 4 (empat) model pembelajaran, diperoleh dosen e dan h memiliki warna yang sama, sehingga kedua dosen dapat memilih model pembelajaran yang sama. Hal ini dapat diartikan jumlah optimal jenis model pembelajaran yang terpilih, dapat disesuaikan dengan banyaknya model pembelajaran yang dipilih dosen.
Pada saat dosen diminta memilih 2 model pembelajaran maka terdapat 3 jenis model pembelajaran, dan pada saat dosen diminta memilih 4 model pembelajaran maka terdapat 5 jenis model pembelajaran. Seperti pada Gambar 1, dosen direpresentasikan sebagai titik dan kelompok riset yang sama direpresentasikan sebagai sisi kemudian dilakukan proses pemberian warna pada titik dikatakan sebagai pewarnaan titik. Proses pemberian warna dengan syarat tertentu disebut pewarnaan titik r-dinamis.
Pewarnaan graf yang lainnya adalah pewarnaan antimagic dinamis dari graf yang didefinisikan sebagai berikut. Fungsi bijektif dengan domain himpunan garis disebut pelabelan antimagic lokal jika dua titik yang berbeda dari graf mempunyai bobot yang berbeda dengan bobot setiap titik sama dengan jumlah semua label dari garis yang terkait dengan titik tersebut.
Pewarnaan r dinamis dari graf G bisa didefinisikan sebagai pemetaan dari v ke himpunan warna sehingga (1) dua titik yang bertetangga dipetakan ke label yang berbeda; (2) untuk setiap titik di graf G kardinalitas dari peta label persekitaran titik tersebut lebih besar sama dengan minimum dari r dan derajat dari titik tersebut. Sedangkan fungsi bijektif dari himpunan garis disebut pewarnaan r dinamis antimagic lokal jika (1) untuk setiap garis uv, bobot u dan bobot v berbeda; (2) untuk setiap titik v, kardinalitas dari bobot persekitaran v lebih besar sama dengan minimum r dan derajat dari titik tersebut. Bilangan kromatik r dinamis antimegic lokal adalah minimum k sehingga graf G mempunyai pewarnaan k titik r dinamis antimagic lokal yang diangkitkan oleh pelabelan antimagic lokal.
Penelitian ini menghasilkan satu lema dan empat teorema. Lema pertama, batas bawah dari bilangan kromatik r dinamis antimagic lokal untuk graf terhubung dengan ordo lebih besar sama dengan 3 adalah 2. Teorema pertama, bilangan kromatik r dinamis antimagic lokal dari graf lintasan berordo n lebih besar sama dengan 2 adalah kurang sama dengan 3 jika r sama dengan 1; untuk r lebih besar sama dengan 2 adalah kurang sama dengan 4,n, (n+4)/3, (n+7)/3, (n+8)/3, (n+9)/3 berturut-turut untuk n sama dengan 5, n sama dengan 3 dan 4, n kongruen 5 modulo 6 dengan n tidak sama dengan 5, n kongruen 2 modulo 6, n kongruen 1 modulo 3 dengan n tidak sama dengan 4, n kelipatan 3 dengan n tidak sama dengan 3.
Teorema kedua, bilangan kromatik r dinamis antimagic lokal dari graf sikel adalah kurang sama dengan 3 untuk r sama dengan 1; untuk r lebih besar sama dengan 2 kurang dari sama dengan n; 2 ditambah bilangan bulat terkecil yang lebih besar sama dengan n/3; 1 ditambah bilangan bulat terkecil yang lebih besar sama dengan n/3 berturut turut untuk n sama dengan 3, 4, 5; n kongruen 1, 2, 3 modulo 6; dan n kongruen 0, 4, 5 modulo 6.
Teorema ketiga, bilangan kromatik r dinamis antimagic lokal dari graf bintang berordo n+1 dengan n lebih besar sama dengan 3 adalah n+1. Teorema keempat, bilangan kromatik r dinamis antimagic lokal dari graf lengkap dengan n lebih besar sama dengan 3 adalah n.
Penulis: Mohammad Imam Utoyo
Artikel lengkapnya dapat diakses melalui laman berikut ini,
https://iopscience.iop.org/article/10.1088/1755-1315/243/1/012077/meta