Teori graf merupakan salah satu cabang ilmu matematika dalam bidang Aljabar. Graf terdiri dari himpunan titik dan himpunan sisi dengan syarat himpunan titik tidak boleh kosong. Sedangkan himpunan sisi memuat pasangan tak teurut dua titik yang berbeda. Salah satu penggunaan graf adalah pewarnaan graf.
Pengertian dari pewarnaan graf adalah proses pemberian warna pada titik atau garis dengan persyaratan tertentu. Salah satu contoh dari pewarnaan graf adalah penentuan konsumsi obat jika terdapat beberapa obat yang tidak dapat dikonsumsi bersama sama oleh penderita suatu penyakit tertentu karena bisa menimbulkan dampak negatif terhadap kesehatannya.
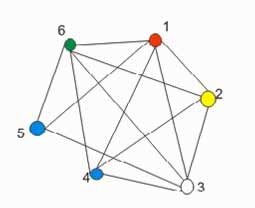
Misalkan ada seorang pasien harus mengkonsumsi 7 jenis obat, yaitu obat 1,2,3,4,5,6,7 sekali dalam satu hari. Diketahui bahwa obat 1 tidak boleh dikonsumsi bersamaan dengan obat 2 dan 4; obat 2 tidak boleh dikonsumsi bersamaan dengan obat 1,4,5,6,7; obat 3 tidak boleh dikonsumsi bersamaan dengan obat 5 dan 7; obat 4 tidak boleh dikonsumsi bersamaan dengan obat 1,6,2; obat 5 tidak boleh dikonsumsi bersamaan dengan obat 2, 3, 7; obat 6 tidak boleh dikonsumsi bersamaan dengan obat 2 dan 4; obat 7 tidak boleh dikonsumsi bersamaan dengan obat 2,3,5. Untuk mengkonsumsi ketujuh jenis obat tersebut perlu direncanakan jumlah jadwal minum obat minimum agar pasien dapat menghemat waktu. Permasalahan ini dapat diselesaikan dengan menggunakan teori graf.
Jika jenis obat dinyatakan dengan titik dan dua titik bertetangga menyatakan dua obat yang tidak bisa dikonsumsi bersama-sama maka permasalahan jadwal minum obat untuk pasien tersebut merupakan permasalahan pewarnaan graf, yaitu pewarnaan titik dengan syarat dua titik yang bertetangga memiliki warna yang berbeda. Dari proses ini diperoleh bahwa jumlah jadwal minimal minum obat bagi pasien tersebut sebanyak tiga kali.
Dengan kata lain, pasien tersebut cukup menyediakan tiga alokasi waktu untuk mengkonsumsi ketujuh obat tersebut dalam satu hari. Jeda antar waktu mengkonsumsi obat-obat tersebut disesuaikan dengan karakter dan sifat dari masing-masing obat. Untuk itu konsultasi dengan dokter juga sangat dianjurkan.
Jenis pewarnaan graf lainnya adalah pewarnaan titik sisi terboboti. Pendefinisian pewarnaan titik sisi terboboti dijelaskan sebagai berikut. Fungsi w dari himpunan garis graf G ke himpunan {1,2,3,…,k} disebut sisi terboboti k dan fungsi Fw di titik v merupakan jumlah semua nilai w(uv) dengan uv merupakan sisi pada graf G. Jika untuk setiap dua titik berbeda u dan v, Fw (u) tidak sama dengan Fw(v) maka sisi terboboti w disebut pewarnaan titik. Nilai minimum k sehingga graf G mempunyai pewarnaan sisi terboboti k dinotasikan dengan µ(G), dan µ disebut bilangan kromatik pewarnaan titik sisi terboboti.
Penelitian ini menghasilkan satu lema dan lima teorema. Lema pertama, bilangan kromatik pewarnaan titik sisi terboboti dari graf hasil korona graf lintasan dengan ordo n lebih besar sama dengan 4 dan graf H adalah lebih besar sama dengan bilangan kromatik pewarnaan titik sisi terboboti graf H. Teorema pertama, bilangan kromatik pewarnaan titik sisi terboboti dari hasil kali korona graf dua lintasan berordo lebih besar sama dengan 4 adalah 2.
Teorema kedua, bilangan kromatik pewarnaan titik sisi terboboti dari hasil kali korona graf lintasan dan graf bintang berordo lebih besar sama dengan 4 adalah 2. Teorema ketiga, bilangan kromatik pewarnaan titik sisi terboboti dari hasil kali korona graf lintasan dan graf kipas berordo lebih besar sama dengan 4 adalah 2.
Teorema keempat, bilangan kromatik pewarnaan titik sisi terboboti dari hasil kali korona graf lintasan dan graf sikel berordo lebih besar sama dengan 3 adalah 2 dan 3 berturut turut untuk ordo kelipatan 4 dan yang lainnya. Teorema kelima, bilangan kromatik pewarnaan titik sisi terboboti dari hasil kali korona graf lintasan dan graf roda berordo lebih besar sama dengan 4 adalah 2.
Penulis: Mohammad Imam Utoyo
Artikel lengkapnya dapat diakses melalui laman berikut,
https://iopscience.iop.org/article/10.1088/1742-6596/1211/1/012004